Nicole Hao

Nicole Hao

AI engineer, CS/math researcher, and technical founder. Passionate about turning research into scalable, everyday tools.

Starshade Station Keeping

Published:

Overview

This project focuses on station keeping for a starshade spacecraft, maintaining precise position and orientation relative to a telescope for exoplanet direct imaging. The work replicates methodologies from “Minimal Differential Lateral Acceleration Configurations for Starshade Stationkeeping” by Jackson Kulik.

Research Context

Station keeping refers to maintaining a spacecraft’s position and orientation relative to a target. For starshade missions, this requires minimizing differential lateral acceleration between the starshade and telescope to ensure precise alignment for scientific observations.

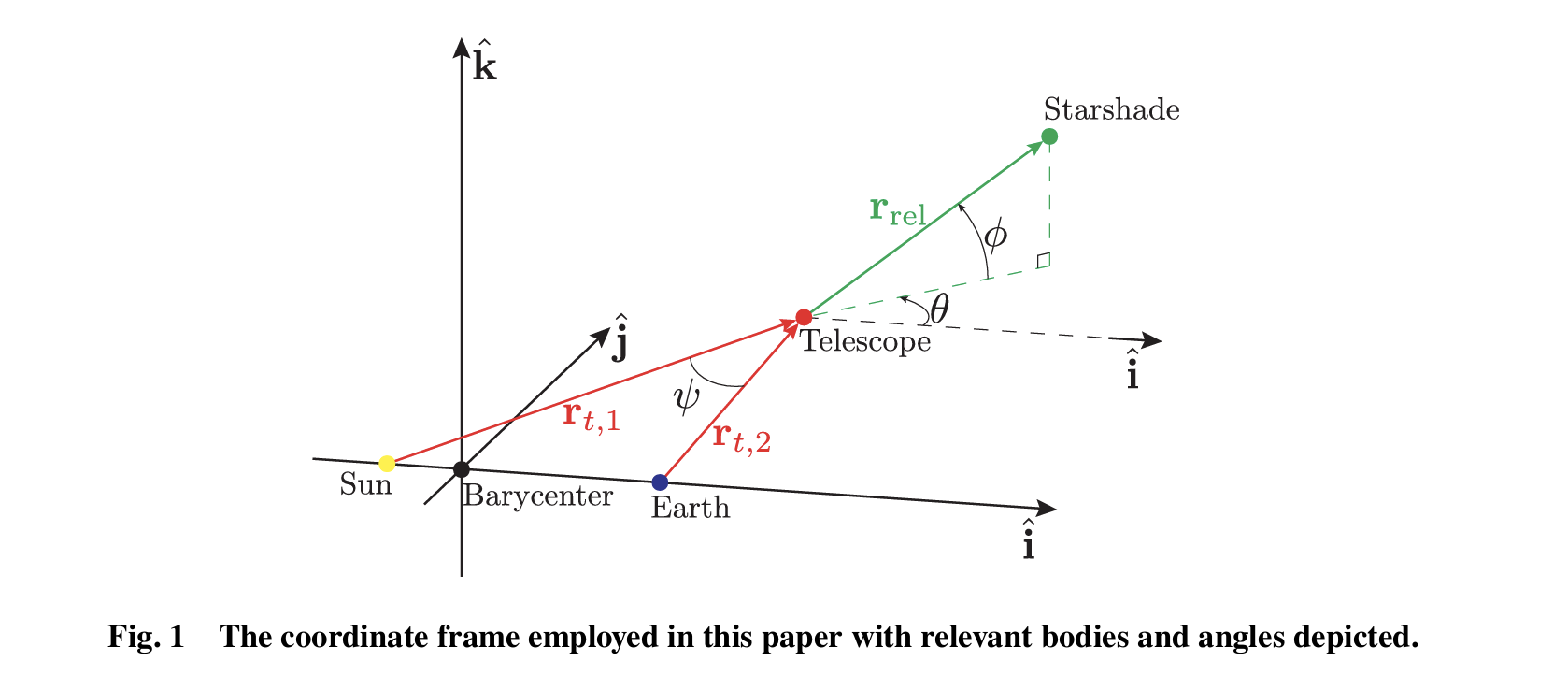
Key Components

1. Orbital Dynamics Simulation

Models the orbital dynamics of the starshade and calculates required adjustments using:

  • Gravitational Force: Newton’s law of gravitation \(F = Gm_1m_2/r^2\)
  • Orbital Perturbations: \(J_2\) perturbation for Earth’s oblateness and third-body interactions
  • Control Maneuvers: Proportional-derivative (PD) control for position maintenance
  • Numerical Integration: 4th-order Runge-Kutta (RK4) method for time evolution

2. Control Algorithm

Implements PD control law for station keeping maneuvers:

  • Computes necessary thruster firings to correct deviations
  • Optimizes fuel consumption while maintaining alignment
  • Continuously monitors position and adjusts in real-time

Mathematical Framework

Orbital Dynamics Equations

The relative motion between starshade and telescope is governed by the two-body problem with perturbations. The equations of motion in the inertial frame:

\[\ddot{\mathbf{r}} = -\frac{\\mu}{r^3}\mathbf{r} + \mathbf{a}_{\text{pert}} + \mathbf{a}_{\text{control}}\]

where: \(\mathbf{r}\) is the position vector

\(\mu = GM\) is the gravitational parameter

\(\mathbf{a}_{\text{pert}}\) represents perturbation accelerations

\(\mathbf{a}_{\text{control}}\) is the control acceleration from thrusters

Gravitational Forces

Newton’s Law of Gravitation:

\[F = \frac{Gm_1m_2}{r^2}\]

The gravitational acceleration between two bodies:

\[\mathbf{a}_{\text{grav}} = -\frac{\mu}{r^3}\mathbf{r}\]

J2 Perturbation Model

Earth’s oblateness causes significant perturbations characterized by the \(J_2\) coefficient:

\[\mathbf{a}_{J_2} = -\frac{3}{2}\frac{J_2\mu R_E^2}{r^4}\begin{bmatrix} x\left(1 - 5\frac{z^2}{r^2}\right) \\\\ y\left(1 - 5\\frac{z^2}{r^2}\right) \\\\ z\left(3 - 5\frac{z^2}{r^2}\right) \end{bmatrix}\]

where: \(J_2 \approx 1.08263 \times 10^{-3} \text{ (Earth's oblateness coefficient)}\)

\[R_E = 6378 \text{km (Earth's equatorial radius)}\] \[(x, y, z) \text{ (position components)}\] \[\text{and } r = \sqrt{x^2 + y^2 + z^2}\]

Alternatively, in terms of orbital elements:

\[\Delta a = -\frac{3}{2}J_2\left(\frac{R_E}{r}\right)^2\left(1 - 3\sin^2\phi\right)\]

where \(\phi\) is the latitude.

Proportional-Derivative (PD) Control Law

The control acceleration is computed using a PD controller:

\[\mathbf{a}_{\text{control}} = k_p\mathbf{e} + k_d\dot{\mathbf{e}}\]

where: \(k_p\) (the proportional gain)

\(k_d\) (the derivative gain)

\(\mathbf{e} = \mathbf{r}{\text{desired}} - \mathbf{r}{\text{actual}}\) (the position error)

\(\dot{\mathbf{e}}\) (the velocity error)

Differential Lateral Acceleration

The key metric for starshade station keeping is minimizing differential lateral acceleration between starshade (S) and telescope (T):

\[\Delta \mathbf{a}_{\perp} = (\mathbf{a}_S - \mathbf{a}_T) - [(\mathbf{a}_S - \mathbf{a}_T) \cdot \hat{\mathbf{r}}_{ST}]\hat{\mathbf{r}}_{ST}\]

where \(\hat{\mathbf{r}}_{ST}\) is the unit vector from telescope to starshade.

Numerical Integration

The equations are solved using the 4th-order Runge-Kutta (RK4) method:

For \(\dot{y} = f(t, y)\):

\[\begin{align} k_1 &= f(t_n, y_n) \\\\ k_2 &= f(t_n + \frac{h}{2}, y_n + \frac{h}{2}k_1) \\\\ k_3 &= f(t_n + \frac{h}{2}, y_n + \frac{h}{2}k_2) \\\\ k_4 &= f(t_n + h, y_n + hk_3) \\\\ y_{n+1} &= y_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4) \end{align}\]

where \(h\) is the time step.

Fuel Optimization Constraint

The total \(\Delta V\) (velocity change) required for station keeping over mission duration \(T\):

\[\Delta V_{\text{total}} = \int_0^T |\mathbf{a}_{\text{control}}(t)| \, dt\]

The goal is to minimize \(\Delta V_{\text{total}}\) while maintaining alignment within tolerance \(\epsilon\):

\[|\mathbf{e}(t)| < \epsilon \quad \forall t \in [0, T]\]

Achievements

  • Accurate simulation of orbital dynamics for station keeping scenarios
  • Efficient control algorithm minimizing fuel usage while maintaining precise alignment (optimizes \(\Delta V_{\text{total}}\))
  • Foundation for understanding station keeping challenges in exoplanet imaging missions
  • Successful replication of results from Kulik et al.’s paper on minimal differential lateral acceleration

Performance Metrics

Key performance indicators for station keeping:

  • Position Error: \(\mathbf{e}< 1\) meter for optimal imaging
  • Differential Acceleration: \(\Delta \mathbf{a}_{\perp}< 10^{-7}\) m/s²
  • Fuel Consumption: Minimized \(\Delta V\) over mission lifetime (typically years)
  • Control Frequency: Adjustments every \(\sim 1\)-10 seconds depending on mission phase

Acknowledgments

Special thanks to Prof. Dmitry Savransky, Prof. Jackson Kulik, and Dr. Grace Genszler at the Cornell Space Imaging and Optical Systems Lab.