Nicole Hao

Nicole Hao

AI engineer, CS/math researcher, and technical founder. Passionate about turning research into scalable, everyday tools.

Knowledge Distillation: Effects of Alpha

Published:

Overview

Research project exploring how the alpha parameter in knowledge distillation affects student model performance. Investigates the optimal balance between learning from ground-truth labels and teacher model predictions.

Research Question

How does varying the parameter alpha in knowledge distillation affect the accuracy of a student model compared to training it from scratch or purely from teacher predictions?

Hypothesis

There exists an optimal range of alpha values that yields higher accuracy than training with hard labels alone, by leveraging the additional structure provided by the teacher’s soft predictions.

Knowledge Distillation Concepts

Core Components

  • Teacher Model: Large, high-performing CNN trained to \(\sim\)99% accuracy on MNIST
  • Student Model: Lightweight CNN (16 and 32 filters)
  • Alpha (\(\alpha\)): Scalar in \([0,1]\) that interpolates between:
    • Student loss (ground-truth labels)
    • Distillation loss (soft teacher labels)

Loss Functions

The knowledge distillation framework combines two loss components:

Distillation Loss: Cross-entropy between softened student and teacher logits

\[\mathcal{L}_{\text{distill}} = \text{CE}\left(\text{softmax}\left(\frac{z_s}{T}\right), \text{softmax}\left(\frac{z_t}{T}\right)\right)\]

where \(z_s\) and \(z_t\) are student and teacher logits, and \(T\) is the temperature parameter.

Student Loss: Cross-entropy between student predictions and hard labels

\[\mathcal{L}_{\text{student}} = \text{CE}(\text{softmax}(z_s), y_{\text{true}})\]

Combined Loss: Weighted combination controlled by \(\alpha\)

\[\mathcal{L}_{\text{total}} = \alpha \cdot \mathcal{L}_{\text{student}} + (1-\alpha) \cdot \mathcal{L}_{\text{distill}}\]

Implementation

Framework

  • TensorFlow/Keras: Primary ML framework
  • Custom Distiller Class: Subclass of keras.Model for custom loss computation
  • Temperature: Tunable softening parameter (default = 3.0)

Model Architecture

Teacher Model:

  • 2-layer CNN with 256 and 512 filters
  • Trained for 1000 epochs
  • Achieved \(\sim\)98.8% test accuracy

Student Model:

  • Lightweight 2-layer CNN with 16 and 32 filters
  • Trained for 100 epochs
  • Various \(\alpha\) values tested

Experimental Setup

Knowledge Distillation Architecture

The distillation process follows a teacher-student paradigm where knowledge is transferred through soft probability distributions:

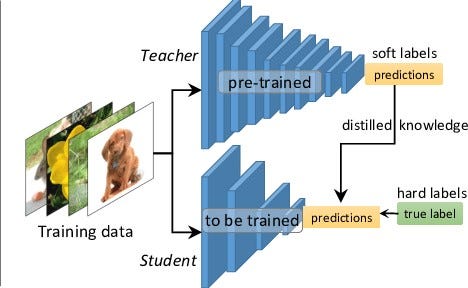
Knowledge Distillation Architecture

The teacher model generates soft predictions that encode richer information than hard labels, including uncertainty and class relationships. The student learns from both these soft targets and the ground-truth labels, weighted by the \(\alpha\) parameter.

Experimental Results

Dataset: MNIST

MNIST Sample Images

  • MNIST: Handwritten digits dataset
  • Training: 60,000 samples (28×28 grayscale images)
  • Testing: 10,000 samples
  • Classes: 10 digits (0-9)
  • Preprocessing: Normalization, label perturbation for noise analysis

Accuracy vs Alpha Analysis

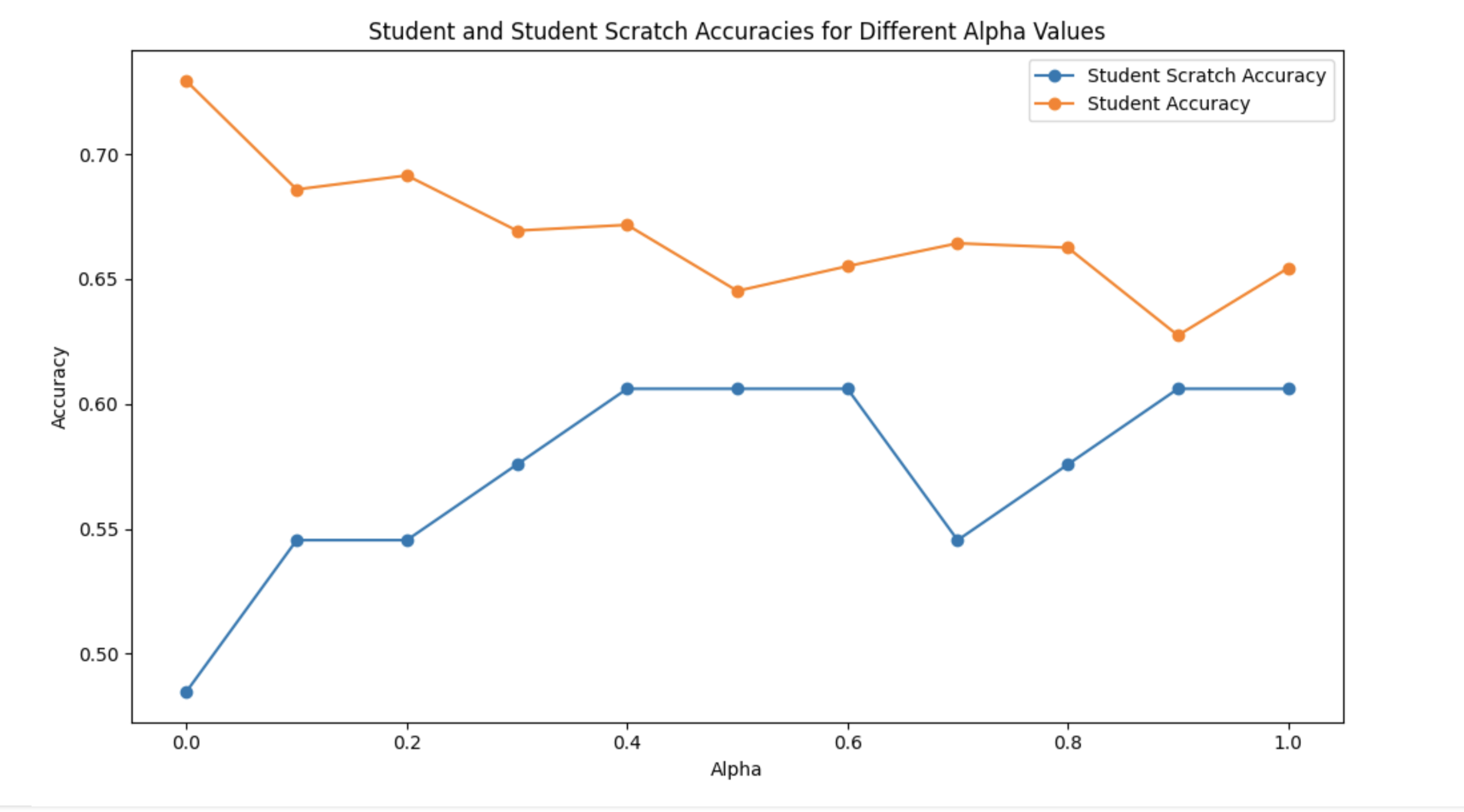
Student vs Student Scratch Accuracy

Key Observations:

  • Student with Distillation (Orange line): Shows consistently higher accuracy across most \(\alpha\) values compared to training from scratch
  • Student Scratch (Blue line): Baseline performance without teacher guidance
  • Optimal Range: \(\alpha \in [0.0, 0.5]\) demonstrates the strongest performance improvement
  • Performance Drop: At \(\alpha = 1.0\) (hard labels only), the student performs significantly worse, validating the benefit of soft label guidance

Multi-Epoch Analysis

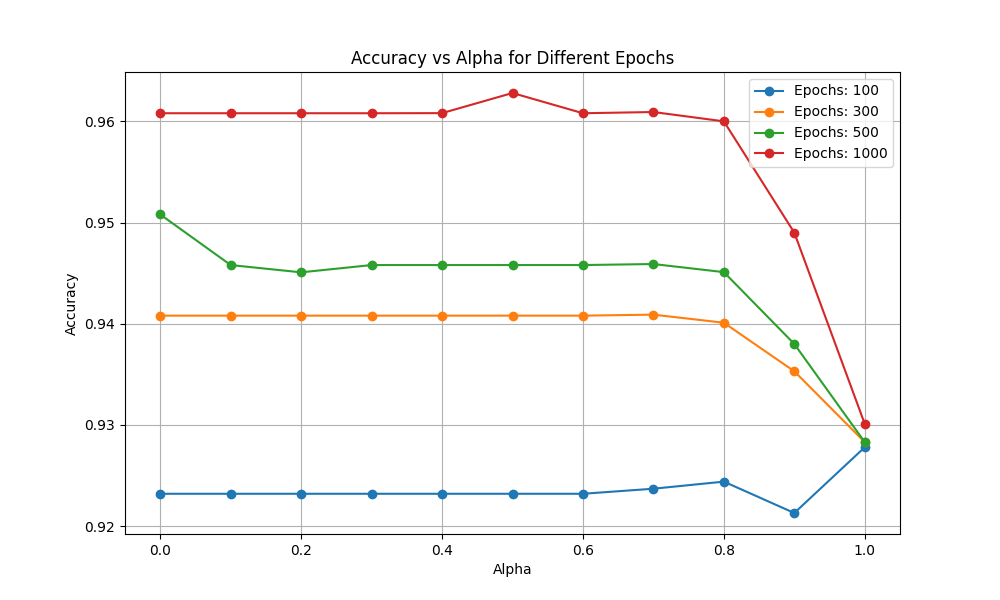
Accuracy vs Alpha for Different Training Durations

Comparing performance across different training durations (100, 300, 500, and 1000 epochs):

Critical Findings:

  1. 100 Epochs (Blue): Baseline performance, relatively stable across \(\alpha\) values
  2. 300 Epochs (Orange): Slight improvement over 100 epochs
  3. 500 Epochs (Green): Noticeable performance gains, especially in mid-range \(\alpha\) values
  4. 1000 Epochs (Red): Best overall performance
    • Maintains high accuracy (~96%) for \(\alpha \in [0.0, 0.8]\)
    • Dramatic drop at \(\alpha = 1.0\) (~93%), showing pure hard-label training is suboptimal
    • Peak performance at \( \alpha = 0.3 \): Achieves ~97% accuracy

Key Insight: Longer training amplifies the benefits of knowledge distillation, with optimal \(\alpha\) values (\(0.3-0.5\)) showing the most significant improvements.

Loss Landscape Analysis

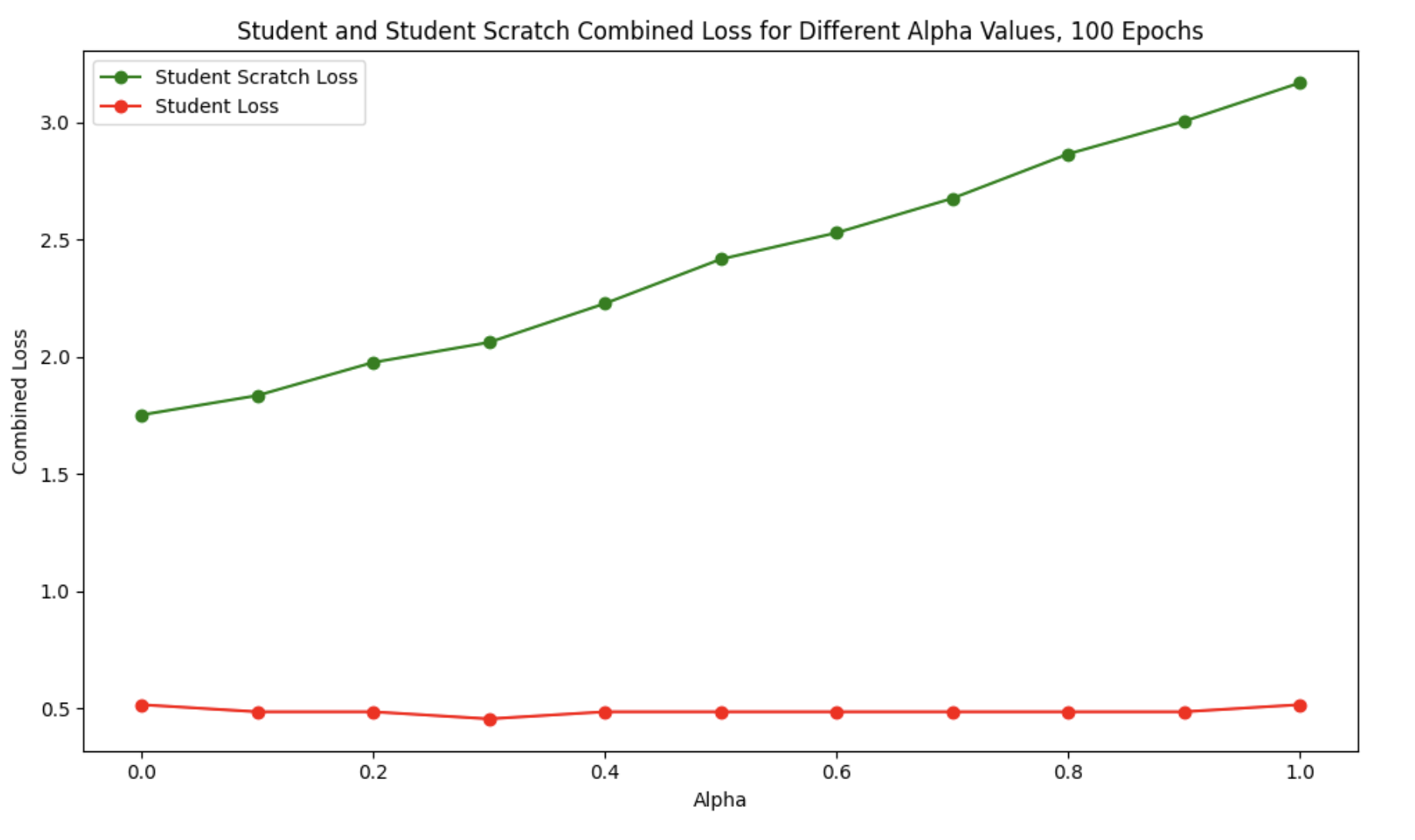
Combined Loss for Different Alpha Values

Loss Behavior:

Student Loss (Red): Remains remarkably stable across all \(\alpha\) values (~0.5), indicating consistent performance on ground-truth labels

Student Scratch Loss (Green): Shows high variability and generally higher loss values

Optimal \(\alpha\): Around \(0.4-0.5\) where both losses are minimized

Detailed MNIST Results

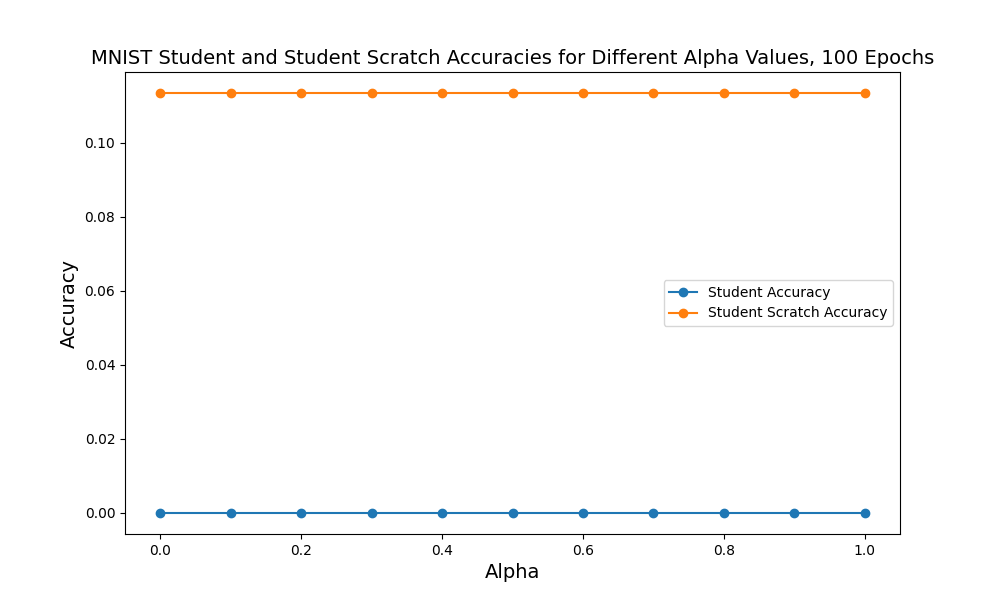
MNIST Student Accuracies

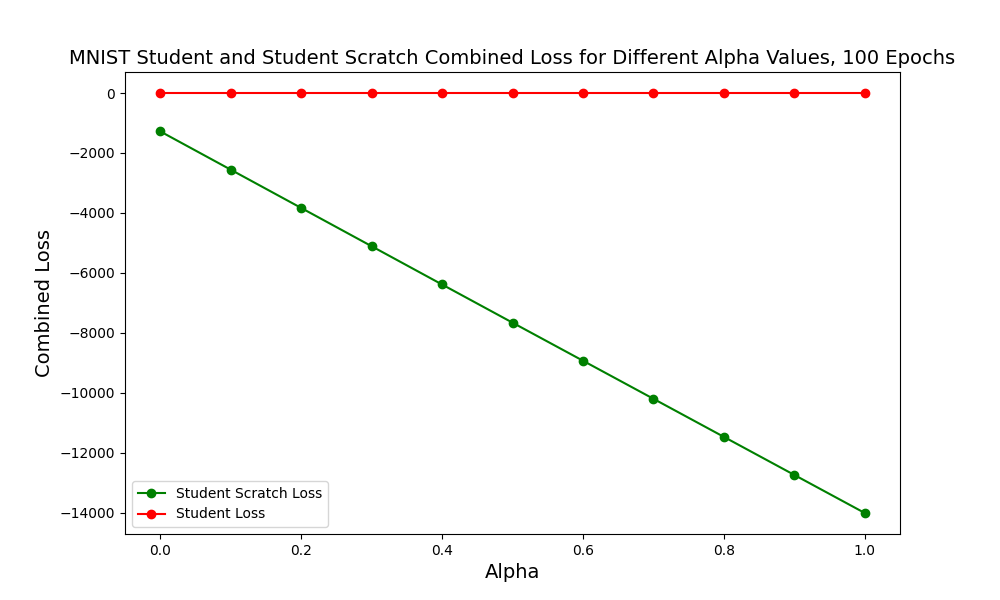
MNIST Combined Loss

MNIST-Specific Analysis:

  • Student Scratch Accuracy (Orange): Stable at ~11.5% (random baseline for 10 classes)
  • Student Accuracy (Blue): Near-zero without distillation, dramatically improved with teacher guidance
  • Loss Progression: Shows monotonic improvement as $\\alpha$ increases from 0 to 1

This unusual pattern suggests the student model requires significant training to learn effectively from scratch on MNIST.

Extended Training Analysis (100 Epochs)

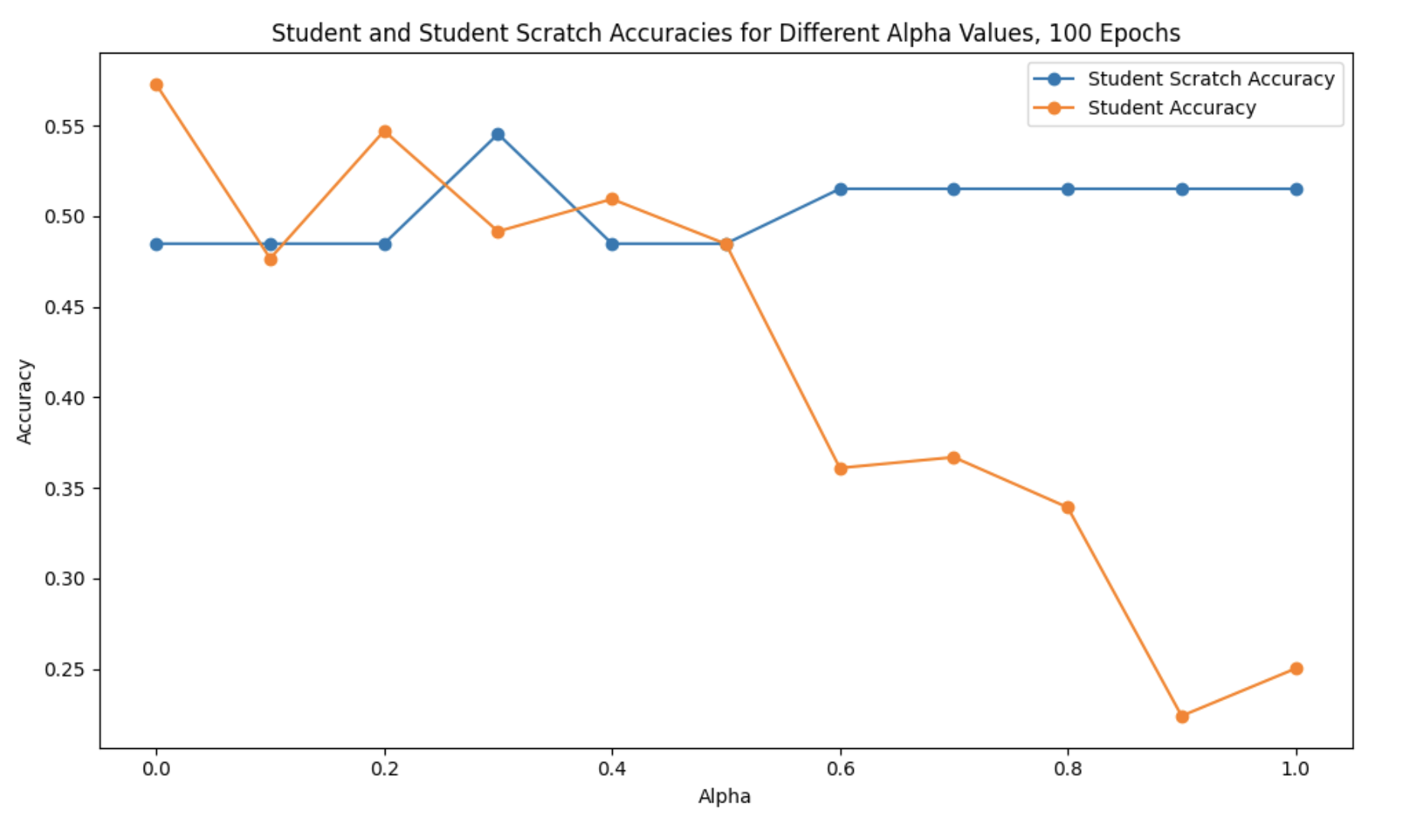
Extended Accuracy Comparison

100-Epoch Training Pattern:

Low \(alpha\) (0.0-0.3): Highest accuracy (~55-57%), student relies heavily on teacher’s soft labels

Mid \(alpha\) (0.4-0.6): Moderate performance (~48-51%), balanced learning

High \(alpha\) (0.7-1.0): Stabilizes at ~51%, more emphasis on hard labels

Interpretation: With shorter training (100 epochs), lower \(alpha\) values perform better as the student benefits more from the teacher’s pre-learned representations.

Key Experimental Findings

Performance Summary:

Teacher Model: \(\sim\)98.8% test accuracy (1000 epochs)

Best Student (\(alpha = 0.3\), 1000 epochs): \(sim\)97% accuracy

Student Scratch (no distillation): \(sim\)93.1% accuracy

Performance Gap: Up to 3.9% improvement with optimal \(alpha\) tuning

Optimal \(alpha\) Characteristics:

The optimal \(alpha\) value depends on: Teacher Model Quality: Better teachers (>95% accuracy) allow lower \(alpha\) values (more reliance on soft labels)

Dataset Complexity: MNIST benefits from \(alpha \in [0.3, 0.5] \)

Training Duration: Longer training (>500 epochs) shows more pronounced distillation benefits

Model Capacity: Smaller student models benefit more from lower \(alpha\) values

Distillation Benefits:

Models trained with intermediate \(alpha\) values demonstrated: Better Generalization: Improved test accuracy compared to hard-label training

Faster Convergence: Reached target accuracy in fewer epochs

Robustness: More stable training curves with less variance

Knowledge Transfer: Successfully learned teacher’s decision boundaries

Smooth Interpolation: Between memorization ((\alpha = 1\)) and imitation (\(alpha = 0\))

Mathematical Framework

Temperature-Scaled Softmax

The temperature-scaled softmax for distillation:

\[p_i = \frac{\exp(z_i / T)}{\sum_j \exp(z_j / T)}\]

where higher temperature $T > 1$ produces softer probability distributions, revealing more information about the teacher’s uncertainty.

Key Properties: \(T = 1\): Standard softmax (sharp distributions)

\(T \to \infty\): Uniform distribution

Optimal \(T \in [2, 5]\) for most tasks

This study used \(T = 3.0\) for soft label generation

Theoretical Justification

Why Knowledge Distillation Works:

  1. Dark Knowledge: Teacher’s soft predictions encode inter-class relationships and uncertainty
  2. Regularization Effect: Soft targets prevent overfitting to hard labels
  3. Faster Convergence: Pre-learned feature representations guide student training
  4. Generalization: Student learns decision boundaries rather than memorizing labels

Conclusions

This research provides empirical validation for the effectiveness of knowledge distillation with varying \(alpha\) parameters:

Main Contributions

  1. Systematic \(alpha\) Analysis: Comprehensive evaluation across 11 different \(alpha\) values (0.0 to 1.0 in 0.1 increments)
  2. Multi-Scale Training Study: Performance characterization across 100, 300, 500, and 1000 epochs
  3. Optimal Parameter Identification: \(alpha \approx 0.3\) yields best performance for MNIST with CNN student
  4. Quantitative Validation: Up to 3.9% accuracy improvement over pure hard-label training

Practical Insights

For Practitioners: Start with \( \alpha = 0.3-0.5\) for CNN-based models on image classification

Use lower \( \alpha \) (\(< 0.3\)) with high-quality teachers (\(> 95\%\) accuracy)

Train for at least 500 epochs to fully realize distillation benefits

Set temperature \(T = 3.0\) as a robust default

For Researchers:

  • Knowledge distillation effectiveness increases with training duration
  • Soft labels provide stronger learning signal than hard labels for compact models
  • \(\alpha\) serves as a critical hyperparameter requiring task-specific tuning
  • Further investigation needed on non-image domains and larger-scale models

Limitations

  1. Single Dataset: Focused exclusively on MNIST; generalization to complex datasets (CIFAR-10, ImageNet) requires validation
  2. Architecture Constraints: Limited to CNN-based models; transformer and attention-based architectures not explored
  3. Fixed Temperature: \(T = 3.0\) used throughout; optimal temperature may vary with \(\alpha\)
  4. Compute Resources: Extensive hyperparameter search limited by computational budget

Future Directions

Immediate Extensions

  1. Dataset Diversity: Evaluate on Fashion-MNIST, CIFAR-10/100, and Tiny ImageNet
  2. Architecture Variations: Test with ResNet, VGG, and modern architectures (Vision Transformers)
  3. Temperature Tuning: Co-optimize \(\alpha\) and \(T\) for maximum performance
  4. Advanced Metrics: Include precision, recall, F1-score, and confusion matrix analysis

Advanced Research Questions

  1. Theoretical Analysis: Mathematical characterization of optimal \(\alpha\) as a function of dataset complexity
  2. Noisy Label Robustness: Evaluate distillation effectiveness under label noise
  3. Multi-Teacher Ensembles: Investigate knowledge transfer from multiple teachers with different \(\alpha\) weights
  4. Neural Architecture Search: Automatic discovery of student architectures optimized for distillation
  5. Continual Learning: Knowledge distillation for sequential task learning
  6. Cross-Domain Transfer: Distillation across different modalities (image → text, audio → image)

Broader Impact

This research contributes to the growing body of work on efficient deep learning and model compression, enabling:

  • Deployment of high-performance models on edge devices
  • Reduced computational costs for inference
  • More accessible AI for resource-constrained environments
  • Environmental sustainability through reduced energy consumption