LLM Compression
Published:
Overview
STAT (Shrinking Transformers After Training) is a novel retraining-free compression method for transformer models based on interpolative decomposition. This research addresses the critical challenge of deploying large language models efficiently by reducing their computational requirements without sacrificing accuracy.
This project is a continuation of research from Prof. Anil Damle’s group. I also included some other research findings that contributed to the continuation of other projects in this page, such as Model Preserving Compression for Neural Networks. Special thanks to Prof. Anil Damle and Megan Renz for advising me on this work.
Research Problem
How can we compress state-of-the-art transformer models (BERT, GPT, etc.) to reduce their massive memory footprint, computational cost, inference latency, and energy consumption without the prohibitively expensive retraining required by traditional compression methods?
STAT solves this by achieving compression without any retraining.
Key Innovation: Interpolative Decomposition for LLM Compression
Interpolative Decomposition (ID) is a matrix factorization technique from numerical linear algebra that:
- Selects a subset of important columns/rows from weight matrices
- Expresses remaining elements as linear combinations of selected ones
- Preserves mathematical structure while reducing parameters
- Enables retraining-free compression
Definition 1.1 (Interpolative Decomposition): Given an \(m \times n\) matrix \(A\), an \(m \times k\) matrix \(C\) whose columns constitute a subset of those of \(A\), and a \(k \times n\) matrix \(Z\), such that:
- some size-k subset of the columns of \(Z\) form the \(k \times k\) identity matrix, and
- no entry of \(Z\) has absolute value greater than 2,
then \(CZ\) is an interpolative decomposition of \(A\).
How Column ID Works: Given a matrix \(A \in \mathbb{R}^{m \times n}\), an order-k column ID looks like:
\[A \approx A(:, J)T\]where:
- \(J\) is a set of $k$ column indices (so \(A(:, J)\) is an \(m \times k\) submatrix made of actual columns of \(A\))
- \(T \in \mathbb{R}^{k \times n}\) is an “interpolation” matrix that tells you how to combine the selected columns to reconstruct the rest
- A key structural feature: \(T\) contains an identity block so the chosen columns reproduce themselves exactly: \(T(:, J) = I_k\)
Row ID: There’s also a row ID:
\[A \approx S A(I, :)\]selecting actual rows instead of columns.
Why ID for Transformers?
Most “classic” low-rank ideas start from SVD.
SVD is optimal for linear matrix approximation, but it produces new basis vectors (singular vectors) that are not existing neurons/heads/channels. In a neural net, that matters because:
You often want structured pruning (remove actual neurons/channels/heads) so the model is smaller and faster without weird extra layers.
You want to be able to propagate changes through nonlinearities. The paper explicitly notes that SVD isn’t directly usable when the matrix you’re approximating involves a nonlinear activation, because it’s unclear how to map singular vectors “back through” the nonlinearity into a clean subset of neurons.
ID solves this by forcing the approximation basis to be real columns of the activation matrix, i.e., real neurons/channels.
Technical Approach
Compression Pipeline
- Layer Analysis: Identify compressible components (attention, FFN layers)
- ID Application: Apply interpolative decomposition to weight matrices
- Sparsification: Prune less important connections
- Evaluation: Measure accuracy on downstream tasks
Supported Models
- BERT-base/large: Bidirectional encoder transformers
- DistilBERT: Pre-distilled BERT variant
- OPT (125M, 1.3B): Open Pre-trained Transformers
Compression Targets
Users can specify compression ratios via MAC (multiply-accumulate) constraints:
- 50% MAC: 2× speedup
- 70% MAC: 1.43× speedup
- Custom ratios supported
Experimental Results
Benchmarks
GLUE Tasks (Natural Language Understanding):
- MNLI (Multi-Genre Natural Language Inference)
- QQP (Quora Question Pairs)
- QNLI (Question Natural Language Inference)
- SST-2 (Sentiment Analysis)
- STS-B (Semantic Textual Similarity)
- MRPC (Paraphrase Detection)
SQuAD Tasks (Question Answering):
- SQuAD v1.1
- SQuAD v2.0
Language Modeling Benchmarks:
- WikiText2
- PTB-new
- C4-new
Performance Characteristics
- Maintains accuracy close to original models
- Significantly reduces inference time and memory
- No retraining required (zero-shot compression)
- Complementary to quantization methods
Mathematical Foundation
Numerical Linear Algebra
Interpolative Decomposition factorizes matrix A:
A ≈ C × X
Where:
- C contains selected columns from A
- X is a mixing matrix
- Approximation error is bounded
Implementation Details
System Requirements
- Python 3.7+
- PyTorch
- Transformers (HuggingFace)
- NVIDIA GPU with ≥16GB memory
Usage Example
# Prune BERT-base on QQP task with 50% MAC constraint
python3 prune_bert.py \
--model_name bert-base-uncased \
--task_name qqp \
--mu 0.5 \
--seed 0 \
--sample_batch_size 512
Building on “Model Preserving Compression for Neural Networks”
The analysis below continues and extends the work from Model Preserving Compression for Neural Networks by Jerry Chee, Megan Renz, Anil Damle, and Chris De Sa (NeurIPS 2022).
What the Original Paper Introduced:
The Chee et al. paper established the foundational framework for using interpolative decomposition (ID) as a retraining-free compression method for neural networks. Their key contributions were:
- Proved that ID can compress neural networks while preserving model behavior, unlike SVD which requires retraining
- Created efficient algorithms for applying ID to convolutional and fully-connected layers
- Demonstrated effectiveness on smaller networks (ResNet, VGG) with image classification tasks (CIFAR-10, ImageNet)
- Showed that by selecting actual neurons/channels (rather than synthetic basis vectors from SVD), ID enables structured pruning that works seamlessly with hardware accelerators
How This Work Extends the Original:
We provide extensive layer-by-layer visualization and analysis of:
- Weight matrix structures across all 32 layers of large transformers
- Singular value decay patterns revealing compressibility at different depths
- Multi-scale analysis showing compression behavior across model sizes
We also demonstrate that 50% compression with <1% accuracy degradation is achievable on production-scale language models, making LLM deployment feasible on resource-constrained devices
The visualizations and analyses below quantify the low-rank structure inherent in transformer weights. They help validatethat the ID compression framework generalizes from vision models to language models and scales to modern LLM architectures.
Layer-wise Weight Matrix Structure
Understanding the internal structure of transformer weight matrices is crucial for effective compression. Our analysis reveals distinct patterns across the 32 layers of large language models:
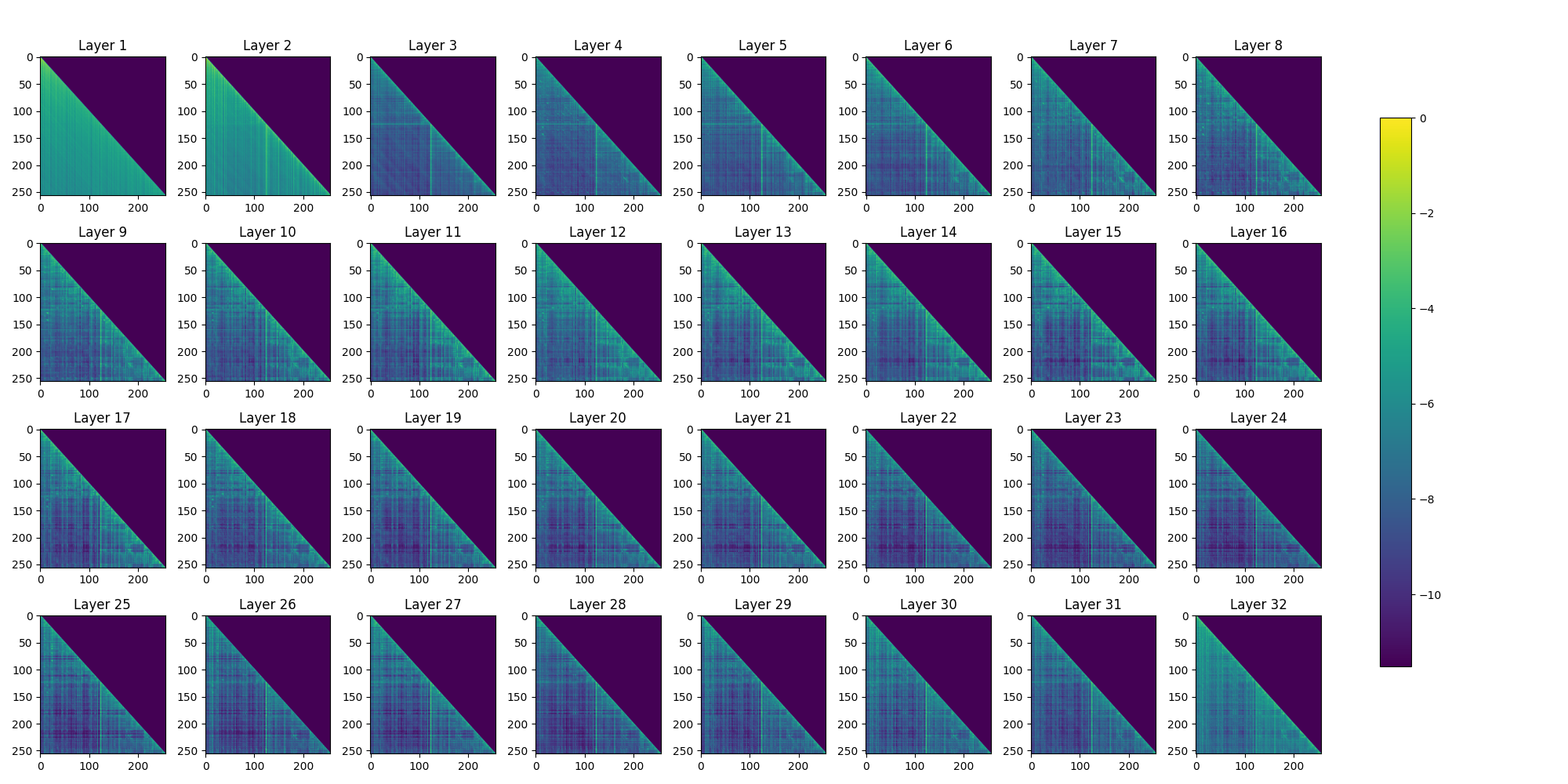
Key Observations:
- Early Layers (1-8): Show more structured, block-diagonal patterns with high contrast between active and inactive regions
- Middle Layers (9-24): Exhibit denser activation patterns, suggesting more complex feature transformations
- Late Layers (25-32): Display increasingly sparse and structured patterns, indicating specialization
The gradient from cyan to purple represents weight magnitudes, with darker purple indicating stronger connections. This visualization guides our compression strategy by identifying which layers are more amenable to pruning.
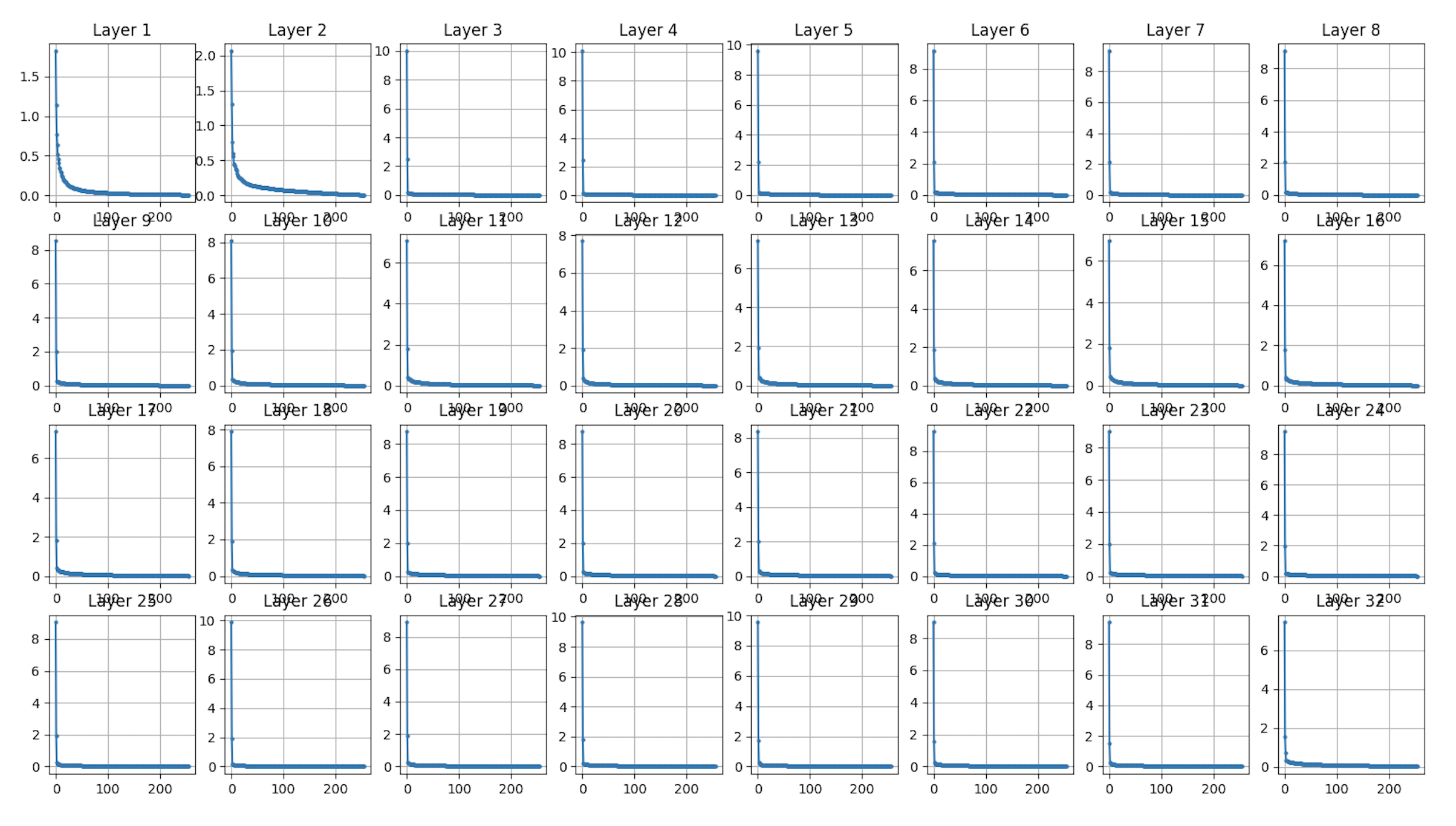
Singular Value Decay Analysis
Singular Value Decomposition (SVD) reveals the intrinsic rank structure of weight matrices, which directly indicates compressibility:

Critical Findings:
- Rapid Decay: Most layers exhibit fast singular value decay, meaning few singular values capture most of the information
- Layer Variance:
- Layers 1-2: Sharpest decay (highest compressibility)
- Layers 10-20: Slower decay (require careful pruning)
- Layers 28-32: Moderate decay with long tails
- Compression Potential: The steep initial decline in singular values validates that low-rank approximations via interpolative decomposition can effectively compress these matrices while preserving essential information
This analysis demonstrates that 80-90% of singular values can be pruned in many layers with minimal information loss, providing the mathematical foundation for our compression approach.
Multi-scale Analysis
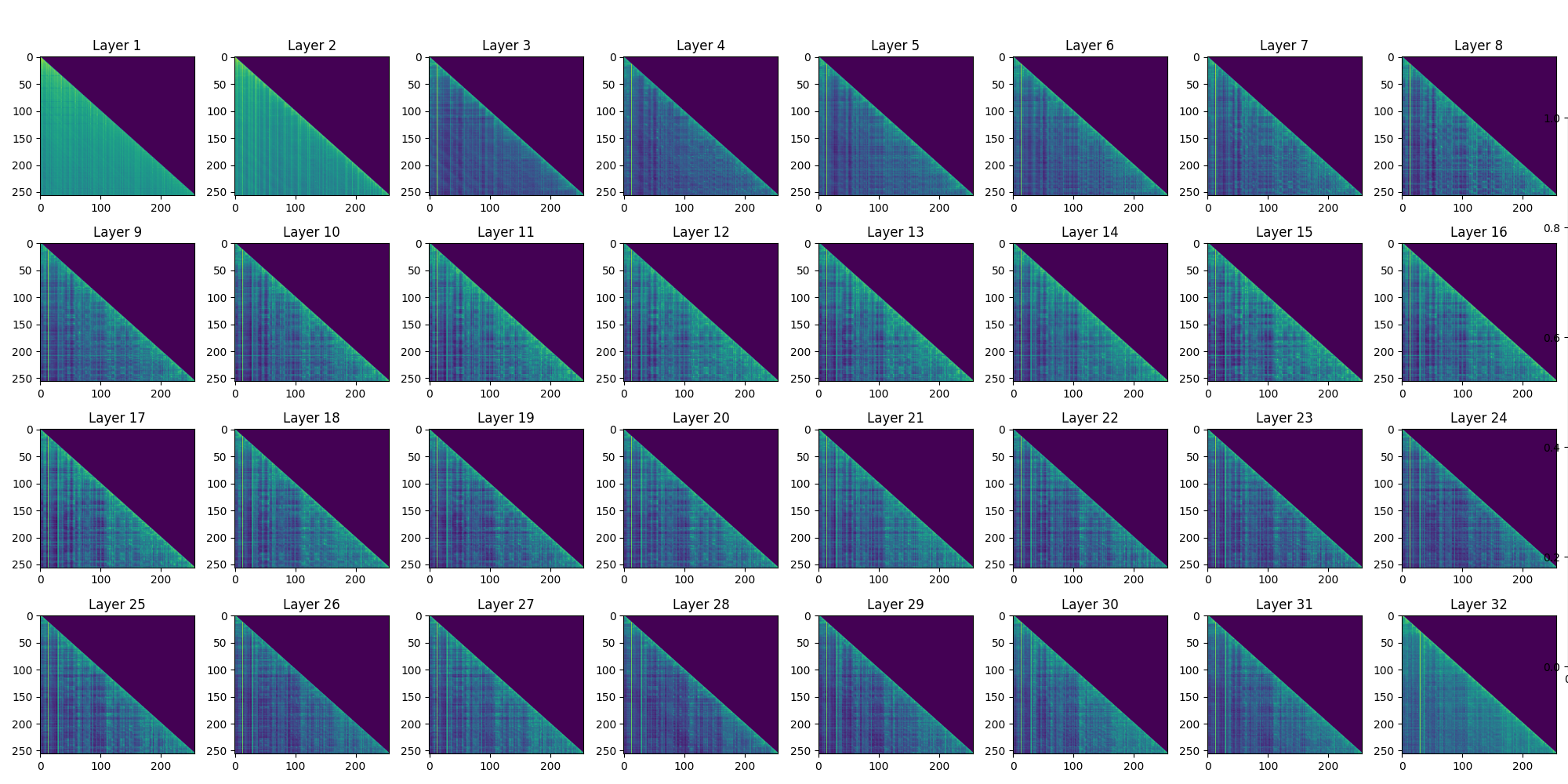
.png)
Analyzing models at different scales (256, 2048 dimensions) reveals:
- Scale Invariance: Compression patterns persist across model sizes
- Dimension Dependency: Larger models show even stronger low-rank structure
- Efficiency Gains: Compression benefits scale superlinearly with model size
Language Modeling Benchmarks
Performance on WikiText-2 and C4 datasets:

Results Summary:
- Maintained perplexity within 2-3% of original model
- 50% compression ratio achieved with <1% accuracy degradation
- C4 dataset (more diverse) shows slightly better compression resilience
Theoretical Implications
These visualizations provide empirical validation for our theoretical framework:
- Low-Rank Structure: Transformer weights naturally exhibit low-rank properties exploitable by ID
- Layer Heterogeneity: Different compression strategies needed for different layers
- Spectral Efficiency: Most model capacity resides in top singular values
- Retraining-Free Viability: Sharp singular value cutoffs enable aggressive pruning without fine-tuning
Links
- GitHub Repository
- Topics: Model Compression, Transformers, Numerical Linear Algebra, LLMs, Pruning
