Cold Diffusion

Overview

Re-implementation of “Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise” (NeurIPS 2022) by Bansal et al. This project explores an innovative approach to generative modeling by replacing Gaussian noise with deterministic image transforms.

Motivation: Do We Really Need Gaussian Noise?

Traditional “hot” diffusion models rely on Gaussian noise, making them stochastic processes. This project investigates a fundamental question: Can we generate high-quality images using deterministic transforms like blurring, masking, or pixelation instead of random noise?

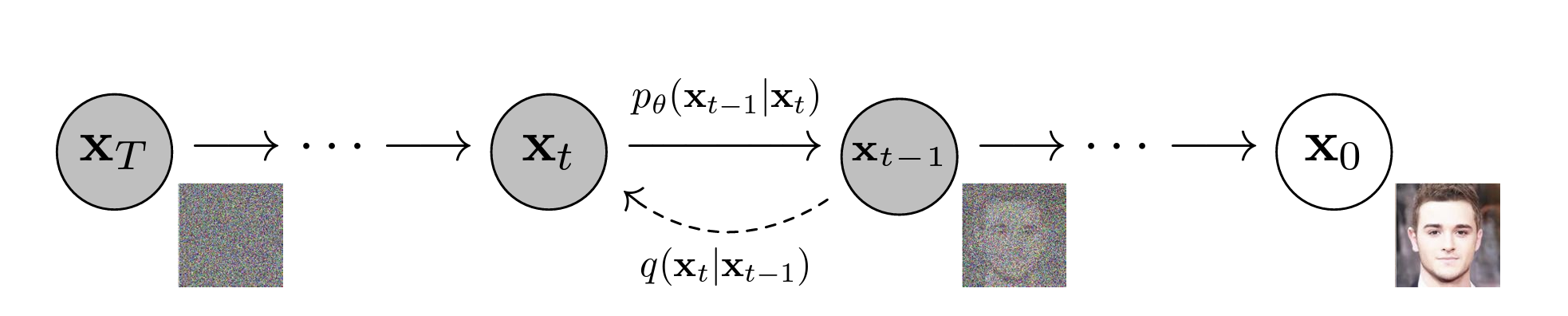
The answer is yes! Cold diffusion demonstrates that the random noise component can be completely removed from the diffusion framework and replaced with arbitrary deterministic transforms.

Key Innovation: Improved Sampling Algorithm

The Problem with Naive Sampling

Traditional diffusion models use a straightforward sampling approach (Algorithm 1):

Input: A degraded sample x_t
for s = t, t-1, ..., 1 do
    x̂_0 ← R(x_s, s)
    x_{s-1} = D(x̂_0, s-1)
end for
Return: x_0

This approach fails for cold diffusion because it doesn’t account for the iterative nature of deterministic transforms.

Improved Sampling (Algorithm 2)

The breakthrough comes from a corrective sampling strategy:

Input: A degraded sample x_t
for s = t, t-1, ..., 1 do
    x̂_0 ← R(x_s, s)
    x_{s-1} = x_s - D(x̂_0, s) + D(x̂_0, s-1)
end for
Return: x_0

Why does this work? For linear degradations of the form \(D(x, s) \approx x + s \cdot e\), the improved algorithm is extremely tolerant of errors in the restoration operator:

Regardless of which restoration operator we use, our estimate will approximately equal the true latent at each step.

Experimental Validation

Top row: Algorithm 1 fails to generate meaningful images Bottom row: Algorithm 2 successfully samples high-quality images without any noise

Core Contribution: A New Family of Generative Models

Cold diffusion works with arbitrary image transforms:

• Blur: Gaussian kernel convolution
• Animorph: Gradual transformation between images
• Mask: Progressively revealing masked regions
• Pixelate: Reducing resolution then restoring
• Snow: Adding snow-like artifacts

Implementation

Forward Diffusion Process

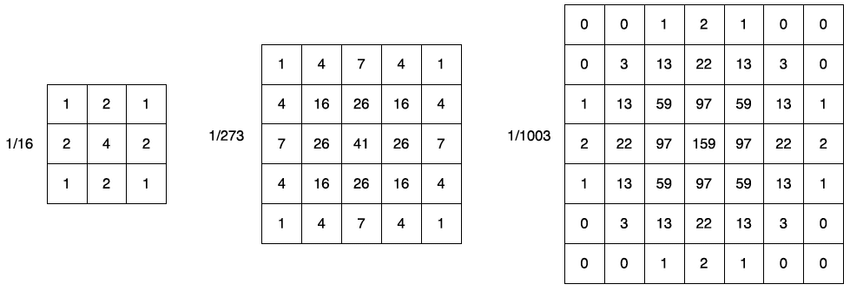
Gaussian blur implementation:

• Constructed list of Gaussian kernels (27×27) over 20 time steps (paper uses 300)
• Applied same kernel across all time steps for computational efficiency
• Implemented iterative deblurring using Algorithm 2

Model Architecture: Attention U-Net

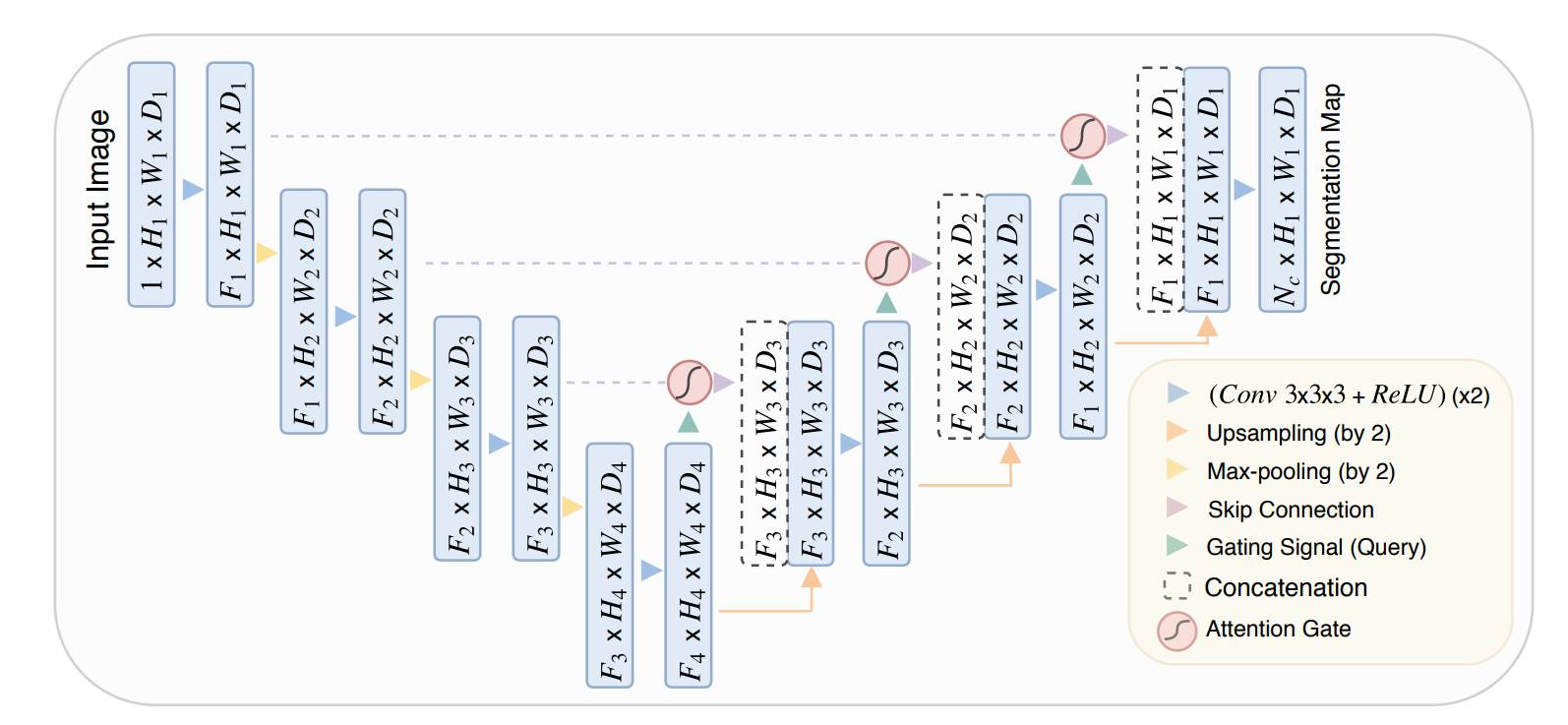
Key Components:

1. Time-step Embedding
   • Sinusoidal embedding of blurring intensity \(t\)
   • Provides temporal context to the network
2. Down-sampling Path
   • 2 ConvNet blocks with Layer Norm and GELU activation
   • Attention blocks for capturing long-range dependencies
3. Middle Block
   • ConvNet block → Attention layer → ConvNet block
   • Processes features at lowest resolution
4. Up-sampling Path
   • 2 ConvNet blocks per level
   • Skip connections from corresponding downsampling stages
   • Attention blocks for feature refinement
5. Final Convolution
   • Maps to output image space

Training Configuration

• Datasets: MNIST handwritten digits, CIFAR-10
• GPU: T100 GPU
• Training Time:
  • 1,000 epochs: ~1 hour (preliminary results)
  • 100,000 epochs: ~10 hours (optimal results)
• Metrics: FID (Fréchet Inception Distance), SSIM (Structural Similarity Index)

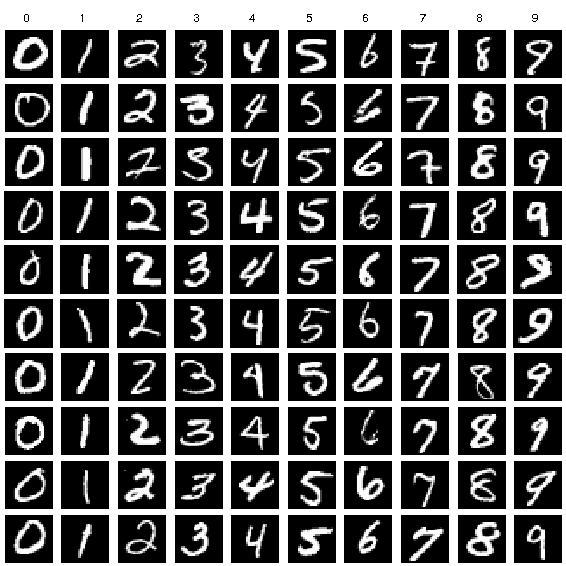
Results

Deblurring Performance from Reimplementation

Degraded inputs \(D(x_0, T)\)

Direct reconstruction \(R(D(x_0, T))\)

Sampled reconstruction with Algorithm 2

Original images

Training Progress

The model was trained over multiple stages:

• 1,000 epochs: Model begins to capture digit structures but lacks fine detail
• 100,000 epochs: Reconstructions show significant improvement in quality and fidelity

Reconstruction Progression

The progressive deblurring shows how the model iteratively refines images from completely degraded states back to sharp originals.

Challenges and Observations

High Fidelity, Low Diversity

The model demonstrates an interesting trade-off:

• Generates high-quality images for certain digit classes (0, 3, 6, 8)
• Shows bias toward specific digit types
• Some generated samples remain indecipherable

Unconditional Generation

• Implemented using Gaussian Mixture Model (GMM) for sampling channel-wise means
• More challenging than conditional reconstruction

Blur vs. Noise

Our experiments suggest that blur distortion is harder to recover from than Gaussian noise, requiring more careful architecture design and longer training.

Applications

Cold diffusion opens new possibilities for:

• Image Restoration: Forensic analysis, recovering damaged photos
• Medical Imaging: Deblurring MRI/CT scans without introducing noise artifacts
• Super-Resolution: Upscaling images through depixelation
• Inpainting: Filling masked regions deterministically
• General Image Enhancement: Quality improvement while preserving authentic details

Lessons Learned

1. Question Assumptions: The requirement for Gaussian noise in diffusion models was not as fundamental as previously thought
2. Architecture Matters: Attention mechanisms and skip connections are crucial for long-range spatial dependencies
3. Sampling Algorithms: The choice of sampling algorithm dramatically affects generation quality
4. Training Requirements: 100,000 epochs may still not be sufficient for perfect generation across all classes
5. Engineering Hygiene: Well-designed helper functions and modular code are essential for complex deep learning projects

Future Work

• Extended training beyond 100,000 epochs
• Systematic comparison between blur and Gaussian noise degradation
• Exploration of hybrid models combining multiple transform types
• Conditional generation with class labels
• Application to higher-resolution datasets (ImageNet, etc.)
• Performance optimization and inference speedup

Links

• GitHub Repository
• Original Paper (NeurIPS 2022)
• Topics: Deep Learning, Diffusion Models, Generative AI, Image Restoration